Post Processing¶
This notebook demonstrates some basic post-processing tasks that can be performed with the Python API, such as plotting a 2D mesh tally and plotting neutron source sites from an eigenvalue calculation. The problem we will use is a simple reflected pin-cell.
[1]:
%matplotlib inline
from IPython.display import Image
import numpy as np
import matplotlib.pyplot as plt
import openmc
Generate Input Files¶
First we need to define materials that will be used in the problem. We’ll create three materials for the fuel, water, and cladding of the fuel pin.
[2]:
# 1.6 enriched fuel
fuel = openmc.Material(name='1.6% Fuel')
fuel.set_density('g/cm3', 10.31341)
fuel.add_nuclide('U235', 3.7503e-4)
fuel.add_nuclide('U238', 2.2625e-2)
fuel.add_nuclide('O16', 4.6007e-2)
# borated water
water = openmc.Material(name='Borated Water')
water.set_density('g/cm3', 0.740582)
water.add_nuclide('H1', 4.9457e-2)
water.add_nuclide('O16', 2.4732e-2)
water.add_nuclide('B10', 8.0042e-6)
# zircaloy
zircaloy = openmc.Material(name='Zircaloy')
zircaloy.set_density('g/cm3', 6.55)
zircaloy.add_nuclide('Zr90', 7.2758e-3)
With our three materials, we can now create a materials file object that can be exported to an actual XML file.
[3]:
# Instantiate a Materials collection
materials = openmc.Materials([fuel, water, zircaloy])
# Export to "materials.xml"
materials.export_to_xml()
Now let’s move on to the geometry. Our problem will have three regions for the fuel, the clad, and the surrounding coolant. The first step is to create the bounding surfaces – in this case two cylinders and six reflective planes.
[4]:
# Create cylinders for the fuel and clad
fuel_outer_radius = openmc.ZCylinder(x0=0.0, y0=0.0, r=0.39218)
clad_outer_radius = openmc.ZCylinder(x0=0.0, y0=0.0, r=0.45720)
# Create boundary planes to surround the geometry
min_x = openmc.XPlane(x0=-0.63, boundary_type='reflective')
max_x = openmc.XPlane(x0=+0.63, boundary_type='reflective')
min_y = openmc.YPlane(y0=-0.63, boundary_type='reflective')
max_y = openmc.YPlane(y0=+0.63, boundary_type='reflective')
min_z = openmc.ZPlane(z0=-0.63, boundary_type='reflective')
max_z = openmc.ZPlane(z0=+0.63, boundary_type='reflective')
With the surfaces defined, we can now create cells that are defined by intersections of half-spaces created by the surfaces.
[5]:
# Create a Universe to encapsulate a fuel pin
pin_cell_universe = openmc.Universe(name='1.6% Fuel Pin')
# Create fuel Cell
fuel_cell = openmc.Cell(name='1.6% Fuel')
fuel_cell.fill = fuel
fuel_cell.region = -fuel_outer_radius
pin_cell_universe.add_cell(fuel_cell)
# Create a clad Cell
clad_cell = openmc.Cell(name='1.6% Clad')
clad_cell.fill = zircaloy
clad_cell.region = +fuel_outer_radius & -clad_outer_radius
pin_cell_universe.add_cell(clad_cell)
# Create a moderator Cell
moderator_cell = openmc.Cell(name='1.6% Moderator')
moderator_cell.fill = water
moderator_cell.region = +clad_outer_radius
pin_cell_universe.add_cell(moderator_cell)
OpenMC requires that there is a “root” universe. Let us create a root cell that is filled by the pin cell universe and then assign it to the root universe.
[6]:
# Create root Cell
root_cell = openmc.Cell(name='root cell')
root_cell.fill = pin_cell_universe
# Add boundary planes
root_cell.region = +min_x & -max_x & +min_y & -max_y & +min_z & -max_z
# Create root Universe
root_universe = openmc.Universe(universe_id=0, name='root universe')
root_universe.add_cell(root_cell)
We now must create a geometry that is assigned a root universe, put the geometry into a geometry file, and export it to XML.
[7]:
# Create Geometry and set root Universe
geometry = openmc.Geometry(root_universe)
[8]:
# Export to "geometry.xml"
geometry.export_to_xml()
With the geometry and materials finished, we now just need to define simulation parameters. In this case, we will use 10 inactive batches and 90 active batches each with 5000 particles.
[9]:
# OpenMC simulation parameters
settings = openmc.Settings()
settings.batches = 100
settings.inactive = 10
settings.particles = 5000
# Create an initial uniform spatial source distribution over fissionable zones
bounds = [-0.63, -0.63, -0.63, 0.63, 0.63, 0.63]
uniform_dist = openmc.stats.Box(bounds[:3], bounds[3:], only_fissionable=True)
settings.source = openmc.Source(space=uniform_dist)
# Export to "settings.xml"
settings.export_to_xml()
Let us also create a plot file that we can use to verify that our pin cell geometry was created successfully.
[10]:
plot = openmc.Plot.from_geometry(geometry)
plot.pixels = (250, 250)
plot.to_ipython_image()
[10]:

As we can see from the plot, we have a nice pin cell with fuel, cladding, and water! Before we run our simulation, we need to tell the code what we want to tally. The following code shows how to create a 2D mesh tally.
[11]:
# Instantiate an empty Tallies object
tallies = openmc.Tallies()
[12]:
# Create mesh which will be used for tally
mesh = openmc.RegularMesh()
mesh.dimension = [100, 100]
mesh.lower_left = [-0.63, -0.63]
mesh.upper_right = [0.63, 0.63]
# Create mesh filter for tally
mesh_filter = openmc.MeshFilter(mesh)
# Create mesh tally to score flux and fission rate
tally = openmc.Tally(name='flux')
tally.filters = [mesh_filter]
tally.scores = ['flux', 'fission']
tallies.append(tally)
[13]:
# Export to "tallies.xml"
tallies.export_to_xml()
Now we a have a complete set of inputs, so we can go ahead and run our simulation.
[14]:
# Run OpenMC!
openmc.run()
%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
############### %%%%%%%%%%%%%%%%%%%%%%%%
################## %%%%%%%%%%%%%%%%%%%%%%%
################### %%%%%%%%%%%%%%%%%%%%%%%
#################### %%%%%%%%%%%%%%%%%%%%%%
##################### %%%%%%%%%%%%%%%%%%%%%
###################### %%%%%%%%%%%%%%%%%%%%
####################### %%%%%%%%%%%%%%%%%%
####################### %%%%%%%%%%%%%%%%%
###################### %%%%%%%%%%%%%%%%%
#################### %%%%%%%%%%%%%%%%%
################# %%%%%%%%%%%%%%%%%
############### %%%%%%%%%%%%%%%%
############ %%%%%%%%%%%%%%%
######## %%%%%%%%%%%%%%
%%%%%%%%%%%
| The OpenMC Monte Carlo Code
Copyright | 2011-2019 MIT and OpenMC contributors
License | http://openmc.readthedocs.io/en/latest/license.html
Version | 0.11.0-dev
Git SHA1 | 61c911cffdae2406f9f4bc667a9a6954748bb70c
Date/Time | 2019-07-19 06:22:24
OpenMP Threads | 4
Reading settings XML file...
Reading cross sections XML file...
Reading materials XML file...
Reading geometry XML file...
Reading U235 from /opt/data/hdf5/nndc_hdf5_v15/U235.h5
Reading U238 from /opt/data/hdf5/nndc_hdf5_v15/U238.h5
Reading O16 from /opt/data/hdf5/nndc_hdf5_v15/O16.h5
Reading H1 from /opt/data/hdf5/nndc_hdf5_v15/H1.h5
Reading B10 from /opt/data/hdf5/nndc_hdf5_v15/B10.h5
Reading Zr90 from /opt/data/hdf5/nndc_hdf5_v15/Zr90.h5
Maximum neutron transport energy: 20000000.000000 eV for U235
Reading tallies XML file...
Writing summary.h5 file...
Initializing source particles...
====================> K EIGENVALUE SIMULATION <====================
Bat./Gen. k Average k
========= ======== ====================
1/1 1.04359
2/1 1.04323
3/1 1.04711
4/1 1.03892
5/1 1.02459
6/1 1.03936
7/1 1.03529
8/1 1.01590
9/1 1.03060
10/1 1.02892
11/1 1.03987
12/1 1.04395 1.04191 +/- 0.00204
13/1 1.04971 1.04451 +/- 0.00285
14/1 1.03880 1.04308 +/- 0.00247
15/1 1.03091 1.04065 +/- 0.00310
16/1 1.03618 1.03990 +/- 0.00264
17/1 1.04109 1.04007 +/- 0.00223
18/1 1.02978 1.03879 +/- 0.00232
19/1 1.06363 1.04155 +/- 0.00344
20/1 1.06549 1.04394 +/- 0.00390
21/1 1.03469 1.04310 +/- 0.00362
22/1 1.01925 1.04111 +/- 0.00386
23/1 1.03268 1.04046 +/- 0.00361
24/1 1.03906 1.04036 +/- 0.00334
25/1 1.02632 1.03943 +/- 0.00325
26/1 1.03906 1.03940 +/- 0.00304
27/1 1.05058 1.04006 +/- 0.00293
28/1 1.03248 1.03964 +/- 0.00279
29/1 1.04076 1.03970 +/- 0.00264
30/1 1.00994 1.03821 +/- 0.00292
31/1 1.04785 1.03867 +/- 0.00281
32/1 1.03080 1.03831 +/- 0.00270
33/1 1.01862 1.03746 +/- 0.00272
34/1 1.05370 1.03813 +/- 0.00269
35/1 1.02226 1.03750 +/- 0.00266
36/1 1.02862 1.03716 +/- 0.00258
37/1 1.04790 1.03755 +/- 0.00251
38/1 1.03762 1.03756 +/- 0.00242
39/1 1.02255 1.03704 +/- 0.00239
40/1 1.06094 1.03784 +/- 0.00245
41/1 1.03842 1.03786 +/- 0.00237
42/1 1.00628 1.03687 +/- 0.00249
43/1 1.04916 1.03724 +/- 0.00245
44/1 1.06237 1.03798 +/- 0.00248
45/1 1.08153 1.03922 +/- 0.00271
46/1 1.05649 1.03970 +/- 0.00268
47/1 1.06265 1.04032 +/- 0.00268
48/1 1.05728 1.04077 +/- 0.00265
49/1 1.07343 1.04161 +/- 0.00271
50/1 1.04640 1.04173 +/- 0.00265
51/1 1.05143 1.04196 +/- 0.00259
52/1 1.03639 1.04183 +/- 0.00253
53/1 1.04846 1.04199 +/- 0.00248
54/1 1.02435 1.04158 +/- 0.00245
55/1 1.04806 1.04173 +/- 0.00240
56/1 1.04798 1.04186 +/- 0.00235
57/1 1.06621 1.04238 +/- 0.00236
58/1 1.05734 1.04269 +/- 0.00233
59/1 1.04581 1.04276 +/- 0.00228
60/1 1.02682 1.04244 +/- 0.00226
61/1 1.05971 1.04278 +/- 0.00224
62/1 1.02357 1.04241 +/- 0.00223
63/1 1.02645 1.04211 +/- 0.00221
64/1 1.00711 1.04146 +/- 0.00226
65/1 1.06171 1.04183 +/- 0.00225
66/1 1.03444 1.04170 +/- 0.00221
67/1 1.05875 1.04199 +/- 0.00219
68/1 1.04640 1.04207 +/- 0.00216
69/1 1.04376 1.04210 +/- 0.00212
70/1 1.07078 1.04258 +/- 0.00214
71/1 1.03916 1.04252 +/- 0.00210
72/1 1.01843 1.04213 +/- 0.00211
73/1 1.03666 1.04205 +/- 0.00207
74/1 1.04625 1.04211 +/- 0.00204
75/1 1.05277 1.04228 +/- 0.00202
76/1 1.04944 1.04238 +/- 0.00199
77/1 1.01898 1.04203 +/- 0.00199
78/1 1.03283 1.04190 +/- 0.00197
79/1 1.02304 1.04163 +/- 0.00196
80/1 1.01539 1.04125 +/- 0.00196
81/1 1.03988 1.04123 +/- 0.00194
82/1 1.02138 1.04096 +/- 0.00193
83/1 1.02473 1.04073 +/- 0.00192
84/1 1.03810 1.04070 +/- 0.00189
85/1 1.07438 1.04115 +/- 0.00192
86/1 1.03048 1.04101 +/- 0.00190
87/1 1.06778 1.04135 +/- 0.00191
88/1 1.07341 1.04177 +/- 0.00192
89/1 1.06729 1.04209 +/- 0.00193
90/1 1.05069 1.04220 +/- 0.00191
91/1 1.07675 1.04262 +/- 0.00193
92/1 1.06470 1.04289 +/- 0.00193
93/1 1.02609 1.04269 +/- 0.00191
94/1 1.04761 1.04275 +/- 0.00189
95/1 1.08802 1.04328 +/- 0.00194
96/1 1.04162 1.04326 +/- 0.00192
97/1 1.04573 1.04329 +/- 0.00190
98/1 1.03232 1.04317 +/- 0.00188
99/1 1.03473 1.04307 +/- 0.00186
100/1 1.04505 1.04309 +/- 0.00184
Creating state point statepoint.100.h5...
=======================> TIMING STATISTICS <=======================
Total time for initialization = 6.4445e-01 seconds
Reading cross sections = 6.1129e-01 seconds
Total time in simulation = 2.0000e+02 seconds
Time in transport only = 1.9970e+02 seconds
Time in inactive batches = 2.9966e+00 seconds
Time in active batches = 1.9701e+02 seconds
Time synchronizing fission bank = 4.0040e-02 seconds
Sampling source sites = 3.1522e-02 seconds
SEND/RECV source sites = 8.3459e-03 seconds
Time accumulating tallies = 9.3582e-03 seconds
Total time for finalization = 4.6582e-02 seconds
Total time elapsed = 2.0072e+02 seconds
Calculation Rate (inactive) = 16685.4 particles/second
Calculation Rate (active) = 2284.19 particles/second
============================> RESULTS <============================
k-effective (Collision) = 1.04342 +/- 0.00159
k-effective (Track-length) = 1.04309 +/- 0.00184
k-effective (Absorption) = 1.04107 +/- 0.00140
Combined k-effective = 1.04195 +/- 0.00117
Leakage Fraction = 0.00000 +/- 0.00000
Tally Data Processing¶
Our simulation ran successfully and created a statepoint file with all the tally data in it. We begin our analysis here loading the statepoint file and ‘reading’ the results. By default, data from the statepoint file is only read into memory when it is requested. This helps keep the memory use to a minimum even when a statepoint file may be huge.
[15]:
# Load the statepoint file
sp = openmc.StatePoint('statepoint.100.h5')
Next we need to get the tally, which can be done with the StatePoint.get_tally(...) method.
[16]:
tally = sp.get_tally(scores=['flux'])
print(tally)
Tally
ID = 1
Name = flux
Filters = MeshFilter
Nuclides = total
Scores = ['flux', 'fission']
Estimator = tracklength
The statepoint file actually stores the sum and sum-of-squares for each tally bin from which the mean and variance can be calculated as described here. The sum and sum-of-squares can be accessed using the sum and sum_sq properties:
[17]:
tally.sum
[17]:
array([[[0.40767451, 0. ]],
[[0.40933814, 0. ]],
[[0.4119165 , 0. ]],
...,
[[0.40854327, 0. ]],
[[0.40970805, 0. ]],
[[0.40948065, 0. ]]])
However, the mean and standard deviation of the mean are usually what you are more interested in. The Tally class also has properties mean and std_dev which automatically calculate these statistics on-the-fly.
[18]:
print(tally.mean.shape)
(tally.mean, tally.std_dev)
(10000, 1, 2)
[18]:
(array([[[0.00452972, 0. ]],
[[0.0045482 , 0. ]],
[[0.00457685, 0. ]],
...,
[[0.00453937, 0. ]],
[[0.00455231, 0. ]],
[[0.00454978, 0. ]]]),
array([[[2.03553236e-05, 0.00000000e+00]],
[[1.83847389e-05, 0.00000000e+00]],
[[1.68647098e-05, 0.00000000e+00]],
...,
[[1.71606078e-05, 0.00000000e+00]],
[[1.87645811e-05, 0.00000000e+00]],
[[1.94447454e-05, 0.00000000e+00]]]))
The tally data has three dimensions: one for filter combinations, one for nuclides, and one for scores. We see that there are 10000 filter combinations (corresponding to the 100 x 100 mesh bins), a single nuclide (since none was specified), and two scores. If we only want to look at a single score, we can use the get_slice(...) method as follows.
[19]:
flux = tally.get_slice(scores=['flux'])
fission = tally.get_slice(scores=['fission'])
print(flux)
Tally
ID = 2
Name = flux
Filters = MeshFilter
Nuclides = total
Scores = ['flux']
Estimator = tracklength
To get the bins into a form that we can plot, we can simply change the shape of the array since it is a numpy array.
[20]:
flux.std_dev.shape = (100, 100)
flux.mean.shape = (100, 100)
fission.std_dev.shape = (100, 100)
fission.mean.shape = (100, 100)
[21]:
fig = plt.subplot(121)
fig.imshow(flux.mean)
fig2 = plt.subplot(122)
fig2.imshow(fission.mean)
[21]:
<matplotlib.image.AxesImage at 0x14d12e58cb38>
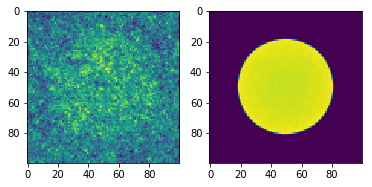
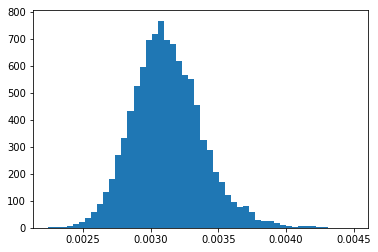
Now let’s say we want to look at the distribution of relative errors of our tally bins for flux. First we create a new variable called relative_error and set it to the ratio of the standard deviation and the mean, being careful not to divide by zero in case some bins were never scored to.
[22]:
# Determine relative error
relative_error = np.zeros_like(flux.std_dev)
nonzero = flux.mean > 0
relative_error[nonzero] = flux.std_dev[nonzero] / flux.mean[nonzero]
# distribution of relative errors
ret = plt.hist(relative_error[nonzero], bins=50)
Source Sites¶
Source sites can be accessed from the source property. As shown below, the source sites are represented as a numpy array with a structured datatype.
[23]:
sp.source
[23]:
array([((-0.28690552, -0.23731283, 0.51447853), ( 0.02705364, -0.14292142, 0.98936422), 1780128.70101981, 1., 0, 0),
((-0.28690552, -0.23731283, 0.51447853), (-0.16786951, 0.86432444, -0.47409186), 1553436.10501094, 1., 0, 0),
(( 0.17162994, 0.134092 , 0.42932363), ( 0.25199134, -0.11168216, 0.96126347), 829530.02360943, 1., 0, 0),
...,
((-0.24444068, -0.01351615, -0.41772172), ( 0.10437178, -0.86754673, 0.486281 ), 807617.55637656, 1., 0, 0),
((-0.2146841 , 0.14307096, 0.07419328), ( 0.89645066, -0.35557279, -0.26446968), 6036005.44157462, 1., 0, 0),
((-0.2146841 , 0.14307096, 0.07419328), (-0.95287644, -0.25857878, 0.15863005), 4923751.04163063, 1., 0, 0)],
dtype=[('r', [('x', '<f8'), ('y', '<f8'), ('z', '<f8')]), ('u', [('x', '<f8'), ('y', '<f8'), ('z', '<f8')]), ('E', '<f8'), ('wgt', '<f8'), ('delayed_group', '<i4'), ('particle', '<i4')])
If we want, say, only the energies from the source sites, we can simply index the source array with the name of the field:
[24]:
sp.source['E']
[24]:
array([1780128.70101981, 1553436.10501094, 829530.02360943, ...,
807617.55637656, 6036005.44157462, 4923751.04163063])
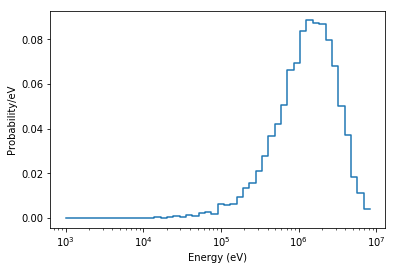
Now, we can look at things like the energy distribution of source sites. Note that we don’t directly use the matplotlib.pyplot.hist method since our binning is logarithmic.
[25]:
# Create log-spaced energy bins from 1 keV to 10 MeV
energy_bins = np.logspace(3,7)
# Calculate pdf for source energies
probability, bin_edges = np.histogram(sp.source['E'], energy_bins, density=True)
# Make sure integrating the PDF gives us unity
print(sum(probability*np.diff(energy_bins)))
# Plot source energy PDF
plt.semilogx(energy_bins[:-1], probability*np.diff(energy_bins), drawstyle='steps')
plt.xlabel('Energy (eV)')
plt.ylabel('Probability/eV')
0.9999999999999999
[25]:
Text(0, 0.5, 'Probability/eV')
Let’s also look at the spatial distribution of the sites. To make the plot a little more interesting, we can also include the direction of the particle emitted from the source and color each source by the logarithm of its energy.
[26]:
plt.quiver(sp.source['r']['x'], sp.source['r']['y'],
sp.source['u']['x'], sp.source['u']['y'],
np.log(sp.source['E']), cmap='jet', scale=20.0)
plt.colorbar()
plt.xlim((-0.5,0.5))
plt.ylim((-0.5,0.5))
[26]:
(-0.5, 0.5)
