Nuclear Data¶
In this notebook, we will go through the salient features of the openmc.data package in the Python API. This package enables inspection, analysis, and conversion of nuclear data from ACE files. Most importantly, the package provides a mean to generate HDF5 nuclear data libraries that are used by the transport solver.
[1]:
%matplotlib inline
import os
from pprint import pprint
import shutil
import subprocess
import urllib.request
import h5py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm
from matplotlib.patches import Rectangle
import openmc.data
Physical Data¶
Some very helpful physical data is available as part of openmc.data: atomic masses, natural abundances, and atomic weights.
[2]:
openmc.data.atomic_mass('Fe54')
[2]:
53.939608306
[3]:
openmc.data.NATURAL_ABUNDANCE['H2']
[3]:
0.00015574
[4]:
openmc.data.atomic_weight('C')
[4]:
12.011115164864455
The IncidentNeutron class¶
The most useful class within the openmc.data API is IncidentNeutron, which stores to continuous-energy incident neutron data. This class has factory methods from_ace, from_endf, and from_hdf5 which take a data file on disk and parse it into a hierarchy of classes in memory. To demonstrate this feature, we will download an ACE file (which can be produced with NJOY 2016) and then load it in using the IncidentNeutron.from_ace method.
[5]:
url = 'https://anl.box.com/shared/static/kxm7s57z3xgfbeq29h54n7q6js8rd11c.ace'
filename, headers = urllib.request.urlretrieve(url, 'gd157.ace')
[6]:
# Load ACE data into object
gd157 = openmc.data.IncidentNeutron.from_ace('gd157.ace')
gd157
[6]:
<IncidentNeutron: Gd157>
Cross sections¶
From Python, it’s easy to explore (and modify) the nuclear data. Let’s start off by reading the total cross section. Reactions are indexed using their “MT” number – a unique identifier for each reaction defined by the ENDF-6 format. The MT number for the total cross section is 1.
[7]:
total = gd157[1]
total
[7]:
<Reaction: MT=1 (n,total)>
Cross sections for each reaction can be stored at multiple temperatures. To see what temperatures are available, we can look at the reaction’s xs attribute.
[8]:
total.xs
[8]:
{'294K': <openmc.data.function.Tabulated1D at 0x1461b4d2f160>}
To find the cross section at a particular energy, 1 eV for example, simply get the cross section at the appropriate temperature and then call it as a function. Note that our nuclear data uses eV as the unit of energy.
[9]:
total.xs['294K'](1.0)
[9]:
142.64747
The xs attribute can also be called on an array of energies.
[10]:
total.xs['294K']([1.0, 2.0, 3.0])
[10]:
array([142.64747 , 38.6541761 , 175.40019642])
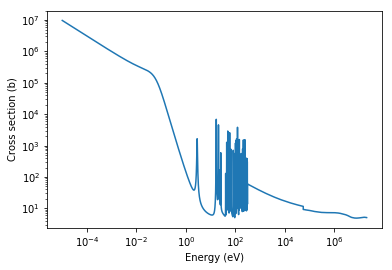
A quick way to plot cross sections is to use the energy attribute of IncidentNeutron. This gives an array of all the energy values used in cross section interpolation for each temperature present.
[11]:
gd157.energy
[11]:
{'294K': array([1.0000e-05, 1.0325e-05, 1.0650e-05, ..., 1.9500e+07, 1.9900e+07,
2.0000e+07])}
[12]:
energies = gd157.energy['294K']
total_xs = total.xs['294K'](energies)
plt.loglog(energies, total_xs)
plt.xlabel('Energy (eV)')
plt.ylabel('Cross section (b)')
[12]:
Text(0, 0.5, 'Cross section (b)')
Reaction Data¶
Most of the interesting data for an IncidentNeutron instance is contained within the reactions attribute, which is a dictionary mapping MT values to Reaction objects.
[13]:
pprint(list(gd157.reactions.values())[:10])
[<Reaction: MT=1 (n,total)>,
<Reaction: MT=101 (n,disappear)>,
<Reaction: MT=301 heating>,
<Reaction: MT=2 (n,elastic)>,
<Reaction: MT=16 (n,2n)>,
<Reaction: MT=17 (n,3n)>,
<Reaction: MT=22 (n,na)>,
<Reaction: MT=24 (n,2na)>,
<Reaction: MT=28 (n,np)>,
<Reaction: MT=41 (n,2np)>]
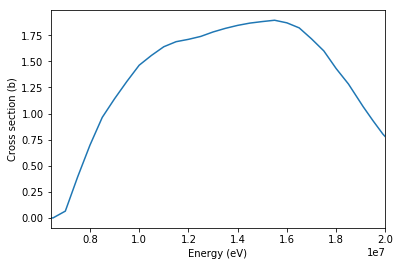
Let’s suppose we want to look more closely at the (n,2n) reaction. This reaction has an energy threshold
[14]:
n2n = gd157[16]
print('Threshold = {} eV'.format(n2n.xs['294K'].x[0]))
Threshold = 6400881.0 eV
The (n,2n) cross section, like all basic cross sections, is represented by the Tabulated1D class. The energy and cross section values in the table can be directly accessed with the x and y attributes. Using the x and y has the nice benefit of automatically acounting for reaction thresholds.
[15]:
n2n.xs
[15]:
{'294K': <openmc.data.function.Tabulated1D at 0x1461b4d594e0>}
[16]:
xs = n2n.xs['294K']
plt.plot(xs.x, xs.y)
plt.xlabel('Energy (eV)')
plt.ylabel('Cross section (b)')
plt.xlim((xs.x[0], xs.x[-1]))
[16]:
(6400881.0, 20000000.0)
To get information on the energy and angle distribution of the neutrons emitted in the reaction, we need to look at the products attribute.
[17]:
n2n.products
[17]:
[<Product: neutron, emission=prompt, yield=polynomial>,
<Product: photon, emission=prompt, yield=tabulated>]
[18]:
neutron = n2n.products[0]
neutron.distribution
[18]:
[<openmc.data.correlated.CorrelatedAngleEnergy at 0x1461b4a66908>]
We see that the neutrons emitted have a correlated angle-energy distribution. Let’s look at the energy_out attribute to see what the outgoing energy distributions are.
[19]:
dist = neutron.distribution[0]
dist.energy_out
[19]:
[<openmc.stats.univariate.Tabular at 0x1461b4d59550>,
<openmc.stats.univariate.Tabular at 0x1461b4d59630>,
<openmc.stats.univariate.Tabular at 0x1461b4d596d8>,
<openmc.stats.univariate.Tabular at 0x1461b4d59828>,
<openmc.stats.univariate.Tabular at 0x1461b4d59a20>,
<openmc.stats.univariate.Tabular at 0x1461b4d59c88>,
<openmc.stats.univariate.Tabular at 0x1461b4d59f98>,
<openmc.stats.univariate.Tabular at 0x1461b4d63358>,
<openmc.stats.univariate.Tabular at 0x1461b4d63748>,
<openmc.stats.univariate.Tabular at 0x1461b4d63ba8>,
<openmc.stats.univariate.Tabular at 0x1461b4d6b0b8>,
<openmc.stats.univariate.Tabular at 0x1461b4d6b588>,
<openmc.stats.univariate.Tabular at 0x1461b4d6bb00>,
<openmc.stats.univariate.Tabular at 0x1461b4aaa0f0>,
<openmc.stats.univariate.Tabular at 0x1461b4aaa710>,
<openmc.stats.univariate.Tabular at 0x1461b4aaad68>,
<openmc.stats.univariate.Tabular at 0x1461b4ab1470>,
<openmc.stats.univariate.Tabular at 0x1461b4ab1b70>,
<openmc.stats.univariate.Tabular at 0x1461b4ab92b0>,
<openmc.stats.univariate.Tabular at 0x1461b4ab9a20>,
<openmc.stats.univariate.Tabular at 0x1461b4ac1208>,
<openmc.stats.univariate.Tabular at 0x1461b4ac19e8>,
<openmc.stats.univariate.Tabular at 0x1461b4ac9240>,
<openmc.stats.univariate.Tabular at 0x1461b4ac9a90>,
<openmc.stats.univariate.Tabular at 0x1461b4acf358>,
<openmc.stats.univariate.Tabular at 0x1461b4acfc18>,
<openmc.stats.univariate.Tabular at 0x1461b4ad7470>,
<openmc.stats.univariate.Tabular at 0x1461b4ad7d30>,
<openmc.stats.univariate.Tabular at 0x1461b4ae0668>,
<openmc.stats.univariate.Tabular at 0x1461b4ae0f98>]
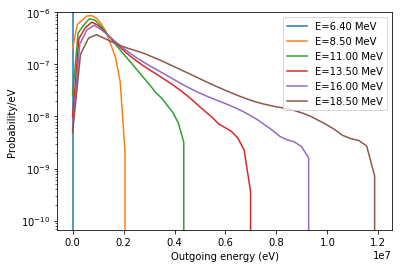
Here we see we have a tabulated outgoing energy distribution for each incoming energy. Note that the same probability distribution classes that we could use to create a source definition are also used within the openmc.data package. Let’s plot every fifth distribution to get an idea of what they look like.
[20]:
for e_in, e_out_dist in zip(dist.energy[::5], dist.energy_out[::5]):
plt.semilogy(e_out_dist.x, e_out_dist.p, label='E={:.2f} MeV'.format(e_in/1e6))
plt.ylim(top=1e-6)
plt.legend()
plt.xlabel('Outgoing energy (eV)')
plt.ylabel('Probability/eV')
plt.show()
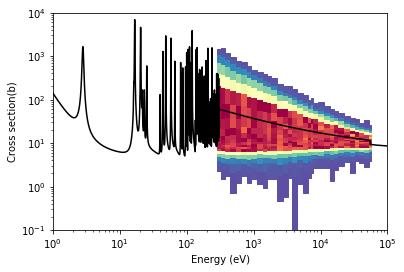
Unresolved resonance probability tables¶
We can also look at unresolved resonance probability tables which are stored in a ProbabilityTables object. In the following example, we’ll create a plot showing what the total cross section probability tables look like as a function of incoming energy.
[21]:
fig = plt.figure()
ax = fig.add_subplot(111)
cm = matplotlib.cm.Spectral_r
# Determine size of probability tables
urr = gd157.urr['294K']
n_energy = urr.table.shape[0]
n_band = urr.table.shape[2]
for i in range(n_energy):
# Get bounds on energy
if i > 0:
e_left = urr.energy[i] - 0.5*(urr.energy[i] - urr.energy[i-1])
else:
e_left = urr.energy[i] - 0.5*(urr.energy[i+1] - urr.energy[i])
if i < n_energy - 1:
e_right = urr.energy[i] + 0.5*(urr.energy[i+1] - urr.energy[i])
else:
e_right = urr.energy[i] + 0.5*(urr.energy[i] - urr.energy[i-1])
for j in range(n_band):
# Determine maximum probability for a single band
max_prob = np.diff(urr.table[i,0,:]).max()
# Determine bottom of band
if j > 0:
xs_bottom = urr.table[i,1,j] - 0.5*(urr.table[i,1,j] - urr.table[i,1,j-1])
value = (urr.table[i,0,j] - urr.table[i,0,j-1])/max_prob
else:
xs_bottom = urr.table[i,1,j] - 0.5*(urr.table[i,1,j+1] - urr.table[i,1,j])
value = urr.table[i,0,j]/max_prob
# Determine top of band
if j < n_band - 1:
xs_top = urr.table[i,1,j] + 0.5*(urr.table[i,1,j+1] - urr.table[i,1,j])
else:
xs_top = urr.table[i,1,j] + 0.5*(urr.table[i,1,j] - urr.table[i,1,j-1])
# Draw rectangle with appropriate color
ax.add_patch(Rectangle((e_left, xs_bottom), e_right - e_left, xs_top - xs_bottom,
color=cm(value)))
# Overlay total cross section
ax.plot(gd157.energy['294K'], total.xs['294K'](gd157.energy['294K']), 'k')
# Make plot pretty and labeled
ax.set_xlim(1.0, 1.0e5)
ax.set_ylim(1e-1, 1e4)
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel('Energy (eV)')
ax.set_ylabel('Cross section(b)')
[21]:
Text(0, 0.5, 'Cross section(b)')
Exporting HDF5 data¶
If you have an instance IncidentNeutron that was created from ACE or HDF5 data, you can easily write it to disk using the export_to_hdf5() method. This can be used to convert ACE to HDF5 or to take an existing data set and actually modify cross sections.
[22]:
gd157.export_to_hdf5('gd157.h5', 'w')
With few exceptions, the HDF5 file encodes the same data as the ACE file.
[23]:
gd157_reconstructed = openmc.data.IncidentNeutron.from_hdf5('gd157.h5')
np.all(gd157[16].xs['294K'].y == gd157_reconstructed[16].xs['294K'].y)
[23]:
True
And one of the best parts of using HDF5 is that it is a widely used format with lots of third-party support. You can use h5py, for example, to inspect the data.
[24]:
h5file = h5py.File('gd157.h5', 'r')
main_group = h5file['Gd157/reactions']
for name, obj in sorted(list(main_group.items()))[:10]:
if 'reaction_' in name:
print('{}, {}'.format(name, obj.attrs['label'].decode()))
reaction_002, (n,elastic)
reaction_016, (n,2n)
reaction_017, (n,3n)
reaction_022, (n,na)
reaction_024, (n,2na)
reaction_028, (n,np)
reaction_041, (n,2np)
reaction_051, (n,n1)
reaction_052, (n,n2)
reaction_053, (n,n3)
[25]:
n2n_group = main_group['reaction_016']
pprint(list(n2n_group.values()))
[<HDF5 group "/Gd157/reactions/reaction_016/294K" (1 members)>,
<HDF5 group "/Gd157/reactions/reaction_016/product_0" (2 members)>,
<HDF5 group "/Gd157/reactions/reaction_016/product_1" (2 members)>]
So we see that the hierarchy of data within the HDF5 mirrors the hierarchy of Python objects that we manipulated before.
[26]:
n2n_group['294K/xs'][()]
[26]:
array([0.000000e+00, 3.026796e-13, 1.291101e-02, 6.511110e-02,
3.926270e-01, 5.752268e-01, 6.969600e-01, 7.399378e-01,
9.635450e-01, 1.142130e+00, 1.308020e+00, 1.463500e+00,
1.557600e+00, 1.640550e+00, 1.688960e+00, 1.711400e+00,
1.739450e+00, 1.782070e+00, 1.816650e+00, 1.845280e+00,
1.865409e+00, 1.867240e+00, 1.881558e+00, 1.881560e+00,
1.881800e+00, 1.894470e+00, 1.869570e+00, 1.821200e+00,
1.716000e+00, 1.600540e+00, 1.431620e+00, 1.283460e+00,
1.101660e+00, 1.065300e+00, 9.307300e-01, 8.029800e-01,
7.777400e-01])
Working with ENDF files¶
In addition to being able to load ACE and HDF5 data, we can also load ENDF data directly into an IncidentNeutron instance using the from_endf() factory method. Let’s download the ENDF/B-VII.1 evaluation for \(^{157}\)Gd and load it in:
[27]:
# Download ENDF file
url = 'https://t2.lanl.gov/nis/data/data/ENDFB-VII.1-neutron/Gd/157'
filename, headers = urllib.request.urlretrieve(url, 'gd157.endf')
# Load into memory
gd157_endf = openmc.data.IncidentNeutron.from_endf(filename)
gd157_endf
[27]:
<IncidentNeutron: Gd157>
Just as before, we can get a reaction by indexing the object directly:
[28]:
elastic = gd157_endf[2]
However, if we look at the cross section now, we see that it isn’t represented as tabulated data anymore.
[29]:
elastic.xs
[29]:
{'0K': <openmc.data.function.ResonancesWithBackground at 0x1461b11824a8>}
If you had Cython installed when you built/installed OpenMC, you should be able to evaluate resonant cross sections from ENDF data directly, i.e., OpenMC will reconstruct resonances behind the scenes for you.
[30]:
elastic.xs['0K'](0.0253)
[30]:
998.7871174521487
When data is loaded from an ENDF file, there is also a special resonances attribute that contains resolved and unresolved resonance region data (from MF=2 in an ENDF file).
[31]:
gd157_endf.resonances.ranges
[31]:
[<openmc.data.resonance.ReichMoore at 0x1461b1fcb898>,
<openmc.data.resonance.Unresolved at 0x1461b2692ba8>]
We see that \(^{157}\)Gd has a resolved resonance region represented in the Reich-Moore format as well as an unresolved resonance region. We can look at the min/max energy of each region by doing the following:
[32]:
[(r.energy_min, r.energy_max) for r in gd157_endf.resonances.ranges]
[32]:
[(1e-05, 306.6), (306.6, 54881.1)]
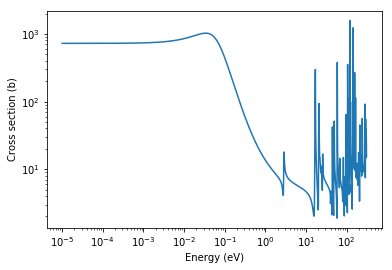
With knowledge of the energy bounds, let’s create an array of energies over the entire resolved resonance range and plot the elastic scattering cross section.
[33]:
# Create log-spaced array of energies
resolved = gd157_endf.resonances.resolved
energies = np.logspace(np.log10(resolved.energy_min),
np.log10(resolved.energy_max), 1000)
# Evaluate elastic scattering xs at energies
xs = elastic.xs['0K'](energies)
# Plot cross section vs energies
plt.loglog(energies, xs)
plt.xlabel('Energy (eV)')
plt.ylabel('Cross section (b)')
[33]:
Text(0, 0.5, 'Cross section (b)')
Resonance ranges also have a useful parameters attribute that shows the energies and widths for resonances.
[34]:
resolved.parameters.head(10)
[34]:
| energy | L | J | neutronWidth | captureWidth | fissionWidthA | fissionWidthB | |
|---|---|---|---|---|---|---|---|
| 0 | 0.0314 | 0 | 2.0 | 0.000474 | 0.1072 | 0.0 | 0.0 |
| 1 | 2.8250 | 0 | 2.0 | 0.000345 | 0.0970 | 0.0 | 0.0 |
| 2 | 16.2400 | 0 | 1.0 | 0.000400 | 0.0910 | 0.0 | 0.0 |
| 3 | 16.7700 | 0 | 2.0 | 0.012800 | 0.0805 | 0.0 | 0.0 |
| 4 | 20.5600 | 0 | 2.0 | 0.011360 | 0.0880 | 0.0 | 0.0 |
| 5 | 21.6500 | 0 | 2.0 | 0.000376 | 0.1140 | 0.0 | 0.0 |
| 6 | 23.3300 | 0 | 1.0 | 0.000813 | 0.1210 | 0.0 | 0.0 |
| 7 | 25.4000 | 0 | 2.0 | 0.001840 | 0.0850 | 0.0 | 0.0 |
| 8 | 40.1700 | 0 | 1.0 | 0.001307 | 0.1100 | 0.0 | 0.0 |
| 9 | 44.2200 | 0 | 2.0 | 0.008960 | 0.0960 | 0.0 | 0.0 |
Heavy-nuclide resonance scattering¶
OpenMC has two methods for accounting for resonance upscattering in heavy nuclides, DBRC and RVS. These methods rely on 0 K elastic scattering data being present. If you have an existing ACE/HDF5 dataset and you need to add 0 K elastic scattering data to it, this can be done using the IncidentNeutron.add_elastic_0K_from_endf() method. Let’s do this with our original gd157 object that we instantiated from an ACE file.
[35]:
gd157.add_elastic_0K_from_endf('gd157.endf')
Let’s check to make sure that we have both the room temperature elastic scattering cross section as well as a 0K cross section.
[36]:
gd157[2].xs
[36]:
{'294K': <openmc.data.function.Tabulated1D at 0x1461b4d2ff60>,
'0K': <openmc.data.function.Tabulated1D at 0x1461b0e59128>}
Generating data from NJOY¶
To run OpenMC in continuous-energy mode, you generally need to have ACE files already available that can be converted to OpenMC’s native HDF5 format. If you don’t already have suitable ACE files or need to generate new data, both the IncidentNeutron and ThermalScattering classes include from_njoy() methods that will run NJOY to generate ACE files and then read those files to create OpenMC class instances. The from_njoy() methods take as input the name
of an ENDF file on disk. By default, it is assumed that you have an executable named njoy available on your path. This can be configured with the optional njoy_exec argument. Additionally, if you want to show the progress of NJOY as it is running, you can pass stdout=True.
Let’s use IncidentNeutron.from_njoy() to run NJOY to create data for \(^2\)H using an ENDF file. We’ll specify that we want data specifically at 300, 400, and 500 K.
[37]:
# Download ENDF file
url = 'https://t2.lanl.gov/nis/data/data/ENDFB-VII.1-neutron/H/2'
filename, headers = urllib.request.urlretrieve(url, 'h2.endf')
# Run NJOY to create deuterium data
h2 = openmc.data.IncidentNeutron.from_njoy('h2.endf', temperatures=[300., 400., 500.], stdout=True)
njoy 2016.49 25Jan19 07/19/19 06:12:49
*****************************************************************************
reconr... 0.0s
broadr... 0.1s
300.0 deg 0.1s
400.0 deg 0.2s
500.0 deg 0.3s
heatr... 0.3s
gaspr... 0.6s
purr... 0.7s
mat = 128 0.7s
---message from purr---mat 128 has no resonance parameters
copy as is to nout
acer... 0.7s
acer... 1.0s
acer... 1.1s
1.2s
*****************************************************************************
Now we can use our h2 object just as we did before.
[38]:
h2[2].xs
[38]:
{'300K': <openmc.data.function.Tabulated1D at 0x1461b066ebe0>,
'400K': <openmc.data.function.Tabulated1D at 0x1461b23a0978>,
'500K': <openmc.data.function.Tabulated1D at 0x1461b1009400>,
'0K': <openmc.data.function.Tabulated1D at 0x1461b101b358>}
Note that 0 K elastic scattering data is automatically added when using from_njoy() so that resonance elastic scattering treatments can be used.
Windowed multipole¶
OpenMC can also be used with an experimental format called windowed multipole. Windowed multipole allows for analytic on-the-fly Doppler broadening of the resolved resonance range. Windowed multipole data can be downloaded with the openmc-get-multipole-data script. This data can be used in the transport solver, but it can also be used directly in the Python API.
[39]:
url = 'https://github.com/mit-crpg/WMP_Library/releases/download/v1.1/092238.h5'
filename, headers = urllib.request.urlretrieve(url, '092238.h5')
[40]:
u238_multipole = openmc.data.WindowedMultipole.from_hdf5('092238.h5')
The WindowedMultipole object can be called with energy and temperature values. Calling the object gives a tuple of 3 cross sections: elastic scattering, radiative capture, and fission.
[41]:
u238_multipole(1.0, 294)
[41]:
(array(9.13284265), array(0.50530278), array(2.9316765e-06))
An array can be passed for the energy argument.
[42]:
E = np.linspace(5, 25, 1000)
plt.semilogy(E, u238_multipole(E, 293.606)[1])
[42]:
[<matplotlib.lines.Line2D at 0x1461b0ed9978>]
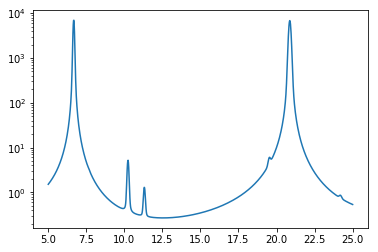
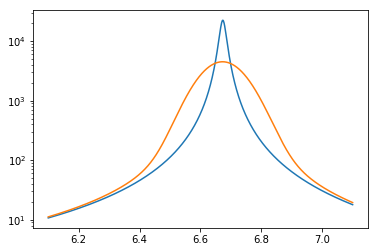
The real advantage to multipole is that it can be used to generate cross sections at any temperature. For example, this plot shows the Doppler broadening of the 6.67 eV resonance between 0 K and 900 K.
[43]:
E = np.linspace(6.1, 7.1, 1000)
plt.semilogy(E, u238_multipole(E, 0)[1])
plt.semilogy(E, u238_multipole(E, 900)[1])
[43]:
[<matplotlib.lines.Line2D at 0x1461b09755c0>]