Multigroup Mode Part I: Introduction¶
This Notebook illustrates the usage of OpenMC’s multi-group calculational mode with the Python API. This example notebook creates and executes the 2-D C5G7 benchmark model using the openmc.MGXSLibrary class to create the supporting data library on the fly.
Generate MGXS Library¶
[1]:
import os
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import numpy as np
import openmc
%matplotlib inline
We will now create the multi-group library using data directly from Appendix A of the C5G7 benchmark documentation. All of the data below will be created at 294K, consistent with the benchmark.
This notebook will first begin by setting the group structure and building the groupwise data for UO2. As you can see, the cross sections are input in the order of increasing groups (or decreasing energy).
Note: The C5G7 benchmark uses transport-corrected cross sections. So the total cross section we input here will technically be the transport cross section.
[2]:
# Create a 7-group structure with arbitrary boundaries (the specific boundaries are unimportant)
groups = openmc.mgxs.EnergyGroups(np.logspace(-5, 7, 8))
uo2_xsdata = openmc.XSdata('uo2', groups)
uo2_xsdata.order = 0
# When setting the data let the object know you are setting the data for a temperature of 294K.
uo2_xsdata.set_total([1.77949E-1, 3.29805E-1, 4.80388E-1, 5.54367E-1,
3.11801E-1, 3.95168E-1, 5.64406E-1], temperature=294.)
uo2_xsdata.set_absorption([8.0248E-03, 3.7174E-3, 2.6769E-2, 9.6236E-2,
3.0020E-02, 1.1126E-1, 2.8278E-1], temperature=294.)
uo2_xsdata.set_fission([7.21206E-3, 8.19301E-4, 6.45320E-3, 1.85648E-2,
1.78084E-2, 8.30348E-2, 2.16004E-1], temperature=294.)
uo2_xsdata.set_nu_fission([2.005998E-2, 2.027303E-3, 1.570599E-2, 4.518301E-2,
4.334208E-2, 2.020901E-1, 5.257105E-1], temperature=294.)
uo2_xsdata.set_chi([5.87910E-1, 4.11760E-1, 3.39060E-4, 1.17610E-7,
0.00000E-0, 0.00000E-0, 0.00000E-0], temperature=294.)
We will now add the scattering matrix data.
Note: Most users familiar with deterministic transport libraries are already familiar with the idea of entering one scattering matrix for every order (i.e. scattering order as the outer dimension). However, the shape of OpenMC’s scattering matrix entry is instead [Incoming groups, Outgoing Groups, Scattering Order] to best enable other scattering representations. We will follow the more familiar approach in this notebook, and then use numpy’s numpy.rollaxis function to change the ordering
to what we need (scattering order on the inner dimension).
[3]:
# The scattering matrix is ordered with incoming groups as rows and outgoing groups as columns
# (i.e., below the diagonal is up-scattering).
scatter_matrix = \
[[[1.27537E-1, 4.23780E-2, 9.43740E-6, 5.51630E-9, 0.00000E-0, 0.00000E-0, 0.00000E-0],
[0.00000E-0, 3.24456E-1, 1.63140E-3, 3.14270E-9, 0.00000E-0, 0.00000E-0, 0.00000E-0],
[0.00000E-0, 0.00000E-0, 4.50940E-1, 2.67920E-3, 0.00000E-0, 0.00000E-0, 0.00000E-0],
[0.00000E-0, 0.00000E-0, 0.00000E-0, 4.52565E-1, 5.56640E-3, 0.00000E-0, 0.00000E-0],
[0.00000E-0, 0.00000E-0, 0.00000E-0, 1.25250E-4, 2.71401E-1, 1.02550E-2, 1.00210E-8],
[0.00000E-0, 0.00000E-0, 0.00000E-0, 0.00000E-0, 1.29680E-3, 2.65802E-1, 1.68090E-2],
[0.00000E-0, 0.00000E-0, 0.00000E-0, 0.00000E-0, 0.00000E-0, 8.54580E-3, 2.73080E-1]]]
scatter_matrix = np.array(scatter_matrix)
scatter_matrix = np.rollaxis(scatter_matrix, 0, 3)
uo2_xsdata.set_scatter_matrix(scatter_matrix, temperature=294.)
Now that the UO2 data has been created, we can move on to the remaining materials using the same process.
However, we will actually skip repeating the above for now. Our simulation will instead use the c5g7.h5 file that has already been created using exactly the same logic as above, but for the remaining materials in the benchmark problem.
For now we will show how you would use the uo2_xsdata information to create an openmc.MGXSLibrary object and write to disk.
[4]:
# Initialize the library
mg_cross_sections_file = openmc.MGXSLibrary(groups)
# Add the UO2 data to it
mg_cross_sections_file.add_xsdata(uo2_xsdata)
# And write to disk
mg_cross_sections_file.export_to_hdf5('mgxs.h5')
Generate 2-D C5G7 Problem Input Files¶
To build the actual 2-D model, we will first begin by creating the materials.xml file.
First we need to define materials that will be used in the problem. In other notebooks, either nuclides or elements were added to materials at the equivalent stage. We can do that in multi-group mode as well. However, multi-group cross-sections are sometimes provided as macroscopic cross-sections; the C5G7 benchmark data are macroscopic. In this case, we can instead use the Material.add_macroscopic method to specify a macroscopic object. Unlike for nuclides and elements, we do not need
provide information on atom/weight percents as no number densities are needed.
When assigning macroscopic objects to a material, the density can still be scaled by setting the density to a value that is not 1.0. This would be useful, for example, when slightly perturbing the density of water due to a small change in temperature (while of course ignoring any resultant spectral shift). The density of a macroscopic dataset is set to 1.0 in the openmc.Material object by default when a macroscopic dataset is used; so we will show its use the first time and then afterwards
it will not be required.
Aside from these differences, the following code is very similar to similar code in other OpenMC example Notebooks.
[5]:
# For every cross section data set in the library, assign an openmc.Macroscopic object to a material
materials = {}
for xs in ['uo2', 'mox43', 'mox7', 'mox87', 'fiss_chamber', 'guide_tube', 'water']:
materials[xs] = openmc.Material(name=xs)
materials[xs].set_density('macro', 1.)
materials[xs].add_macroscopic(xs)
Now we can go ahead and produce a materials.xml file for use by OpenMC
[6]:
# Instantiate a Materials collection, register all Materials, and export to XML
materials_file = openmc.Materials(materials.values())
# Set the location of the cross sections file to our pre-written set
materials_file.cross_sections = 'c5g7.h5'
materials_file.export_to_xml()
Our next step will be to create the geometry information needed for our assembly and to write that to the geometry.xml file.
We will begin by defining the surfaces, cells, and universes needed for each of the individual fuel pins, guide tubes, and fission chambers.
[7]:
# Create the surface used for each pin
pin_surf = openmc.ZCylinder(x0=0, y0=0, R=0.54, name='pin_surf')
# Create the cells which will be used to represent each pin type.
cells = {}
universes = {}
for material in materials.values():
# Create the cell for the material inside the cladding
cells[material.name] = openmc.Cell(name=material.name)
# Assign the half-spaces to the cell
cells[material.name].region = -pin_surf
# Register the material with this cell
cells[material.name].fill = material
# Repeat the above for the material outside the cladding (i.e., the moderator)
cell_name = material.name + '_moderator'
cells[cell_name] = openmc.Cell(name=cell_name)
cells[cell_name].region = +pin_surf
cells[cell_name].fill = materials['water']
# Finally add the two cells we just made to a Universe object
universes[material.name] = openmc.Universe(name=material.name)
universes[material.name].add_cells([cells[material.name], cells[cell_name]])
The next step is to take our universes (representing the different pin types) and lay them out in a lattice to represent the assembly types
[8]:
lattices = {}
# Instantiate the UO2 Lattice
lattices['UO2 Assembly'] = openmc.RectLattice(name='UO2 Assembly')
lattices['UO2 Assembly'].dimension = [17, 17]
lattices['UO2 Assembly'].lower_left = [-10.71, -10.71]
lattices['UO2 Assembly'].pitch = [1.26, 1.26]
u = universes['uo2']
g = universes['guide_tube']
f = universes['fiss_chamber']
lattices['UO2 Assembly'].universes = \
[[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, u, u, g, u, u, g, u, u, g, u, u, u, u, u],
[u, u, u, g, u, u, u, u, u, u, u, u, u, g, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, g, u, u, g, u, u, g, u, u, g, u, u, g, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, g, u, u, g, u, u, f, u, u, g, u, u, g, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, g, u, u, g, u, u, g, u, u, g, u, u, g, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, g, u, u, u, u, u, u, u, u, u, g, u, u, u],
[u, u, u, u, u, g, u, u, g, u, u, g, u, u, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u],
[u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u, u]]
# Create a containing cell and universe
cells['UO2 Assembly'] = openmc.Cell(name='UO2 Assembly')
cells['UO2 Assembly'].fill = lattices['UO2 Assembly']
universes['UO2 Assembly'] = openmc.Universe(name='UO2 Assembly')
universes['UO2 Assembly'].add_cell(cells['UO2 Assembly'])
# Instantiate the MOX Lattice
lattices['MOX Assembly'] = openmc.RectLattice(name='MOX Assembly')
lattices['MOX Assembly'].dimension = [17, 17]
lattices['MOX Assembly'].lower_left = [-10.71, -10.71]
lattices['MOX Assembly'].pitch = [1.26, 1.26]
m = universes['mox43']
n = universes['mox7']
o = universes['mox87']
g = universes['guide_tube']
f = universes['fiss_chamber']
lattices['MOX Assembly'].universes = \
[[m, m, m, m, m, m, m, m, m, m, m, m, m, m, m, m, m],
[m, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, m],
[m, n, n, n, n, g, n, n, g, n, n, g, n, n, n, n, m],
[m, n, n, g, n, o, o, o, o, o, o, o, n, g, n, n, m],
[m, n, n, n, o, o, o, o, o, o, o, o, o, n, n, n, m],
[m, n, g, o, o, g, o, o, g, o, o, g, o, o, g, n, m],
[m, n, n, o, o, o, o, o, o, o, o, o, o, o, n, n, m],
[m, n, n, o, o, o, o, o, o, o, o, o, o, o, n, n, m],
[m, n, g, o, o, g, o, o, f, o, o, g, o, o, g, n, m],
[m, n, n, o, o, o, o, o, o, o, o, o, o, o, n, n, m],
[m, n, n, o, o, o, o, o, o, o, o, o, o, o, n, n, m],
[m, n, g, o, o, g, o, o, g, o, o, g, o, o, g, n, m],
[m, n, n, n, o, o, o, o, o, o, o, o, o, n, n, n, m],
[m, n, n, g, n, o, o, o, o, o, o, o, n, g, n, n, m],
[m, n, n, n, n, g, n, n, g, n, n, g, n, n, n, n, m],
[m, n, n, n, n, n, n, n, n, n, n, n, n, n, n, n, m],
[m, m, m, m, m, m, m, m, m, m, m, m, m, m, m, m, m]]
# Create a containing cell and universe
cells['MOX Assembly'] = openmc.Cell(name='MOX Assembly')
cells['MOX Assembly'].fill = lattices['MOX Assembly']
universes['MOX Assembly'] = openmc.Universe(name='MOX Assembly')
universes['MOX Assembly'].add_cell(cells['MOX Assembly'])
# Instantiate the reflector Lattice
lattices['Reflector Assembly'] = openmc.RectLattice(name='Reflector Assembly')
lattices['Reflector Assembly'].dimension = [1,1]
lattices['Reflector Assembly'].lower_left = [-10.71, -10.71]
lattices['Reflector Assembly'].pitch = [21.42, 21.42]
lattices['Reflector Assembly'].universes = [[universes['water']]]
# Create a containing cell and universe
cells['Reflector Assembly'] = openmc.Cell(name='Reflector Assembly')
cells['Reflector Assembly'].fill = lattices['Reflector Assembly']
universes['Reflector Assembly'] = openmc.Universe(name='Reflector Assembly')
universes['Reflector Assembly'].add_cell(cells['Reflector Assembly'])
Let’s now create the core layout in a 3x3 lattice where each lattice position is one of the assemblies we just defined.
After that we can create the final cell to contain the entire core.
[9]:
lattices['Core'] = openmc.RectLattice(name='3x3 core lattice')
lattices['Core'].dimension= [3, 3]
lattices['Core'].lower_left = [-32.13, -32.13]
lattices['Core'].pitch = [21.42, 21.42]
r = universes['Reflector Assembly']
u = universes['UO2 Assembly']
m = universes['MOX Assembly']
lattices['Core'].universes = [[u, m, r],
[m, u, r],
[r, r, r]]
# Create boundary planes to surround the geometry
min_x = openmc.XPlane(x0=-32.13, boundary_type='reflective')
max_x = openmc.XPlane(x0=+32.13, boundary_type='vacuum')
min_y = openmc.YPlane(y0=-32.13, boundary_type='vacuum')
max_y = openmc.YPlane(y0=+32.13, boundary_type='reflective')
# Create root Cell
root_cell = openmc.Cell(name='root cell')
root_cell.fill = lattices['Core']
# Add boundary planes
root_cell.region = +min_x & -max_x & +min_y & -max_y
# Create root Universe
root_universe = openmc.Universe(name='root universe', universe_id=0)
root_universe.add_cell(root_cell)
Before we commit to the geometry, we should view it using the Python API’s plotting capability
[10]:
root_universe.plot(origin=(0., 0., 0.), width=(3 * 21.42, 3 * 21.42), pixels=(500, 500),
color_by='material')
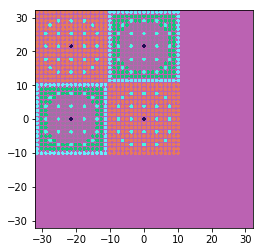
OK, it looks pretty good, let’s go ahead and write the file
[11]:
# Create Geometry and set root Universe
geometry = openmc.Geometry(root_universe)
# Export to "geometry.xml"
geometry.export_to_xml()
We can now create the tally file information. The tallies will be set up to give us the pin powers in this notebook. We will do this with a mesh filter, with one mesh cell per pin.
[12]:
tallies_file = openmc.Tallies()
# Instantiate a tally Mesh
mesh = openmc.RegularMesh()
mesh.dimension = [17 * 2, 17 * 2]
mesh.lower_left = [-32.13, -10.71]
mesh.upper_right = [+10.71, +32.13]
# Instantiate tally Filter
mesh_filter = openmc.MeshFilter(mesh)
# Instantiate the Tally
tally = openmc.Tally(name='mesh tally')
tally.filters = [mesh_filter]
tally.scores = ['fission']
# Add tally to collection
tallies_file.append(tally)
# Export all tallies to a "tallies.xml" file
tallies_file.export_to_xml()
With the geometry and materials finished, we now just need to define simulation parameters for the settings.xml file. Note the use of the energy_mode attribute of our settings_file object. This is used to tell OpenMC that we intend to run in multi-group mode instead of the default continuous-energy mode. If we didn’t specify this but our cross sections file was not a continuous-energy data set, then OpenMC would complain.
This will be a relatively coarse calculation with only 500,000 active histories. A benchmark-fidelity run would of course require many more!
[13]:
# OpenMC simulation parameters
batches = 150
inactive = 50
particles = 5000
# Instantiate a Settings object
settings_file = openmc.Settings()
settings_file.batches = batches
settings_file.inactive = inactive
settings_file.particles = particles
# Tell OpenMC this is a multi-group problem
settings_file.energy_mode = 'multi-group'
# Set the verbosity to 6 so we dont see output for every batch
settings_file.verbosity = 6
# Create an initial uniform spatial source distribution over fissionable zones
bounds = [-32.13, -10.71, -1e50, 10.71, 32.13, 1e50]
uniform_dist = openmc.stats.Box(bounds[:3], bounds[3:], only_fissionable=True)
settings_file.source = openmc.Source(space=uniform_dist)
# Tell OpenMC we want to run in eigenvalue mode
settings_file.run_mode = 'eigenvalue'
# Export to "settings.xml"
settings_file.export_to_xml()
Let’s go ahead and execute the simulation! You’ll notice that the output for multi-group mode is exactly the same as for continuous-energy. The differences are all under the hood.
[14]:
# Run OpenMC
openmc.run()
%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%
############### %%%%%%%%%%%%%%%%%%%%%%%%
################## %%%%%%%%%%%%%%%%%%%%%%%
################### %%%%%%%%%%%%%%%%%%%%%%%
#################### %%%%%%%%%%%%%%%%%%%%%%
##################### %%%%%%%%%%%%%%%%%%%%%
###################### %%%%%%%%%%%%%%%%%%%%
####################### %%%%%%%%%%%%%%%%%%
####################### %%%%%%%%%%%%%%%%%
###################### %%%%%%%%%%%%%%%%%
#################### %%%%%%%%%%%%%%%%%
################# %%%%%%%%%%%%%%%%%
############### %%%%%%%%%%%%%%%%
############ %%%%%%%%%%%%%%%
######## %%%%%%%%%%%%%%
%%%%%%%%%%%
| The OpenMC Monte Carlo Code
Copyright | 2011-2017 Massachusetts Institute of Technology
License | http://openmc.readthedocs.io/en/latest/license.html
Version | 0.8.0
Git SHA1 | 966169de084fcfda3a5aaca3edc0065c8caf6bbc
Date/Time | 2017-03-09 08:18:02
OpenMP Threads | 8
Reading settings XML file...
Reading geometry XML file...
Reading materials XML file...
Reading cross sections HDF5 file...
Reading tallies XML file...
Loading cross section data...
Loading uo2 data...
Loading mox43 data...
Loading mox7 data...
Loading mox87 data...
Loading fiss_chamber data...
Loading guide_tube data...
Loading water data...
Building neighboring cells lists for each surface...
Initializing source particles...
====================> K EIGENVALUE SIMULATION <====================
Creating state point statepoint.150.h5...
=======================> TIMING STATISTICS <=======================
Total time for initialization = 1.3630E-01 seconds
Reading cross sections = 3.0827E-02 seconds
Total time in simulation = 8.9648E+00 seconds
Time in transport only = 8.2752E+00 seconds
Time in inactive batches = 2.4798E+00 seconds
Time in active batches = 6.4849E+00 seconds
Time synchronizing fission bank = 1.4553E-02 seconds
Sampling source sites = 1.0318E-02 seconds
SEND/RECV source sites = 4.0840E-03 seconds
Time accumulating tallies = 4.2427E-04 seconds
Total time for finalization = 1.7081E-02 seconds
Total time elapsed = 9.1340E+00 seconds
Calculation Rate (inactive) = 1.00813E+05 neutrons/second
Calculation Rate (active) = 77101.8 neutrons/second
============================> RESULTS <============================
k-effective (Collision) = 1.18880 +/- 0.00179
k-effective (Track-length) = 1.18853 +/- 0.00244
k-effective (Absorption) = 1.18601 +/- 0.00111
Combined k-effective = 1.18628 +/- 0.00111
Leakage Fraction = 0.00175 +/- 0.00006
[14]:
0
Results Visualization¶
Now that we have run the simulation, let’s look at the fission rate and flux tallies that we tallied.
[15]:
# Load the last statepoint file and keff value
sp = openmc.StatePoint('statepoint.' + str(batches) + '.h5')
# Get the OpenMC pin power tally data
mesh_tally = sp.get_tally(name='mesh tally')
fission_rates = mesh_tally.get_values(scores=['fission'])
# Reshape array to 2D for plotting
fission_rates.shape = mesh.dimension
# Normalize to the average pin power
fission_rates /= np.mean(fission_rates[fission_rates > 0.])
# Force zeros to be NaNs so their values are not included when matplotlib calculates
# the color scale
fission_rates[fission_rates == 0.] = np.nan
# Plot the pin powers and the fluxes
plt.figure()
plt.imshow(fission_rates, interpolation='none', cmap='jet', origin='lower')
plt.colorbar()
plt.title('Pin Powers')
plt.show()
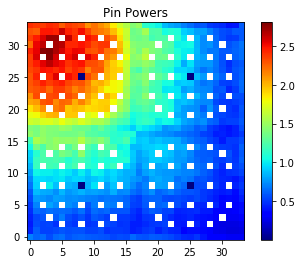
There we have it! We have just successfully run the C5G7 benchmark model!